（3）A1C1、とCB1、A2C2と、CB2、A3C3とCB3の交点それぞれG1、G2、G3とすれば、C,G1,G2,G3,Bを結ぶ曲線は正円弧キャンバとなる。

7.1.3 擬円弧キャンバを描く（その1）

（1）半幅AB、キャンバ高さACにおいて、Aを中心に半径ACの弧を描き、ABとの交点をDとする。

（2）AD、弧CD、ABのそれぞれを等分するが、例えば4等分するものとする。それぞれの等分点をE,F,G,H,I,J及びE',F',G'とする。

（3）ABと垂直にE',F',G'に立てた垂線上において、E'H'＝EH、F'I'＝FI、G'J'＝GJとなるようにH',I',J',をとる。これらとB,Cを結ぶ曲線は擬円弧キャンバとなる。

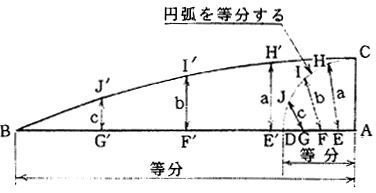
図1.31

7.1.4 擬円弧キャンバを描く（その2）

（1）前述の7.1.3に似た方法であるが、E,F,Gの求め方が異なる。即ち、船体中心線上にAK＝2ACとなる点Kをとり、Kと弧CDの等分点H,I,Jを結ぶことにより、E,F,Gを求める。その後は、7.1.3と同じである。

（2）AK＝2ACの代りにAK＝ACとしてKを求め、後は上記（1）と同じ手順で擬円弧キャンバを描く方法もある。

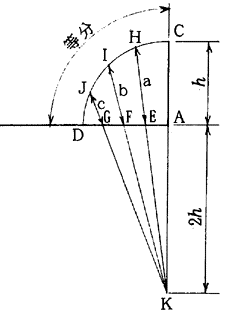
図1.32

7.2 シヤー

7.2.1 拠物線シヤーを描く

（1）シヤー高さをAB、甲板舷側線におけるシヤー止り迄の距離をACとするACには適当な縮尺を用いる。AB,ACを等分するが、ここでは5等分するものとし、それぞれの等分点をB1,B2,B3,B4及びC1,C2,C3,C4とする。

（2）CからB1、B2、B3、B4に引いた直線とAC上にC1,C2,C3,C4にて立てた垂線との順次対応する交点をD1,D2,D3,D4とすれば、これらとB,Cを結ぶ曲線は拠物線シヤーとなる。

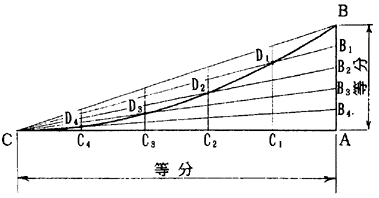
図1.33

前ページ　　　目次へ　　　次ページ